Addition via Logic Gates

 

Review: Multiple-bit Binary Addition

 
carry 111
0011
+ 0101
sum 1000
↓

One-bit Binary Addition

 
0 0 1 1
+ 0 + 1 + 0 + 1
00 01 01 10
→
carry, sum 0, 0 0, 1 0, 1 1, 0
inputoutput
ABcarrysum
0000
0101
1001
1110

What do these results look like?

One-bit Addition

inputoutput
ABcarrysum
0000
0101
1001
1110
 
sum = A XOR B
carry = A AND B
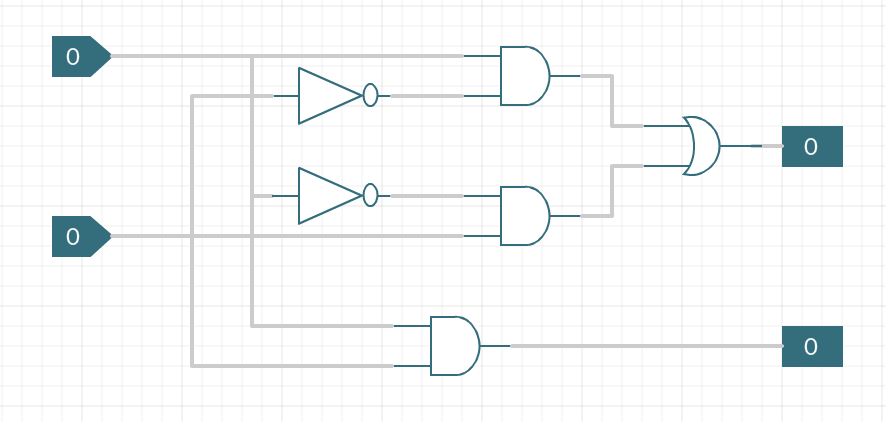
Half-Adder Circuit Diagram
We can also draw this using the other XOR circuit diagram or an XOR gate.

NOTE: This does not allow for a carry-in! What about if we want to add numbers that have more than one bit?

This does only half of the total task, and is known as a half-adder.

Binary Addition with carry-in

The way humans do it...

 
0 0 1 1 0 0 1 1
+ 0 + 1 + 0 + 1 + 0 + 1 + 0 + 1
00 01 01 10 00 01 01 10
carry-in + 0 + 0 + 0 + 0 + 1 + 1 + 1 + 1
00 01 01 10 01 10 10 11
 
carry, sum 0, 0 0, 1 0, 1 1, 0 0, 1 1, 0 1, 0 1, 1

 

The way computers do it with half-adders

 
First HA 0 0 1 1 0 0 1 1
+ 0 + 1 + 0 + 1 + 0 + 1 + 0 + 1
carry, sum 0, 0 0, 1 0, 1 1, 0 0, 0 0, 1 0, 1 1, 0
  ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓
 
Second HA 0 1 1 0 0 1 1 0
carry-in + 0 + 0 + 0 + 0 + 1 + 1 + 1 + 1
carry, sum 0, 0 0, 1 0, 1 0, 0 0, 1 1, 0 1, 0 0, 1
Full carry, sum       1, 0   1, 0 1, 0 1, 1

Sum bit: sum bit from the second HA

Carry bit: true if either HA generated a carry

 

Summary: One-bit Addition With Carry-in

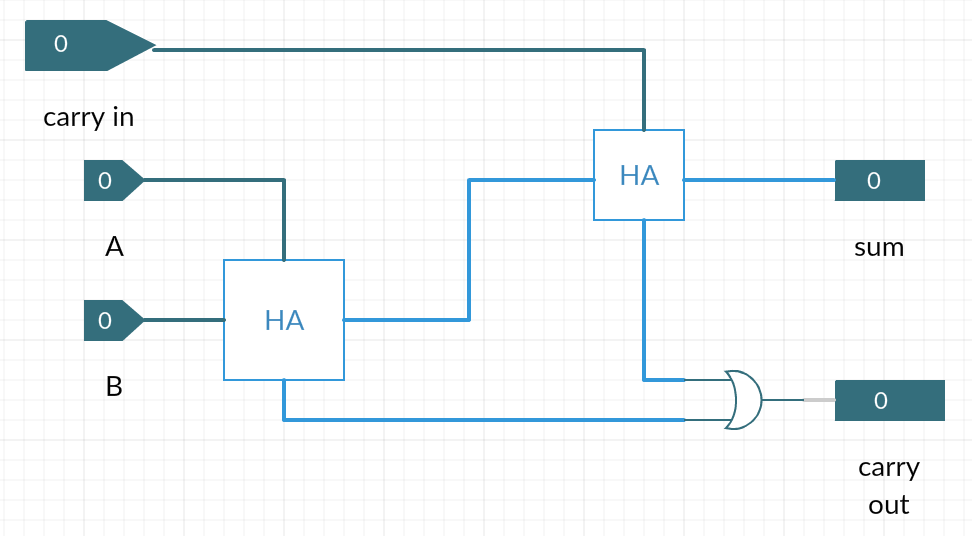
Full-Adder Circuit Diagram

We have two half-adders. The first adds A + B. The sum bit of that is then added to the carryin in the second half-adder. The overall sum is the sum bit from the second add.

sumfull = carryin XOR sumh1

The addition yields a carry if either of the two half-adders yield a carry.

carryout = carryh1 OR carryh2

Next: How do we set up a multi-bit adder?
Alyce Brady, Kalamazoo College