Lab: Finite State Automata and Regular Expressions
Finite State Automata
This lab should be done individually, although you may certainly discuss your progress with your neighbors.
A finite state machine is said to accept a given input string if the input takes the machine from the start state, indicated in these diagrams by a triangle, to an accepting (or final) state, indicated by a double border.
We will be dealing with relatively simple finite state automata that are easily drawn by hand. If you wish, you may use JFLAP, a graphical tool for experimenting with concepts from automata theory, to check your work. You can access JFLAP on-line at www.jflap.org. Download the first version listed, "JFLAP_Thin.jar". (Click here for a simple "cheat sheet" on using JFLAP.)
Write down answers to each of the numbered questions below. First, try answering these questions without building the machines in JFLAP. Feel free to use JFLAP to check your answers.
- Consider the following FSA:
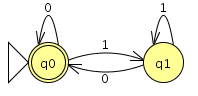
- 1. Will this machine accept the string
1001? Will it accept0010?- 2. Write down two additional strings that this FSA will accept.
- 3. Write down two additional strings that this FSA will reject.
- 4. Provide an English language description of the set of strings that this FSA accepts.
- 2. Write down two additional strings that this FSA will accept.
- 1. Will this machine accept the string
- Consider the following FSA:
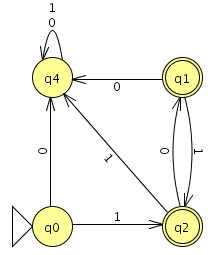
- 5. Will this machine accept the string
1010? Will it accept01010?1010110?- 6. Write down two additional strings that this FSA will accept.
- 7. Write down two additional strings that this FSA will reject.
- 8. Provide an English language description of the set of strings that this FSA accepts.
- 6. Write down two additional strings that this FSA will accept.
- 5. Will this machine accept the string
- Using JFLAP, design and test FSAs that recognize the following two sets.
Once you are satisfied that they work, draw the FSAs on your answer sheet.
- 9. The set of all strings of 0's and 1's that end in a 1.
- 10. The set of all strings of 0's and 1's with an odd length.
- 9. The set of all strings of 0's and 1's that end in a 1.
Regular Expressions
Regular expressions provide another way of describing the sets of
strings that are "accepted" by a finite state machine, i.e.,
for which the finite state machine will halt in an "accept" state.
Binary strings are just sequences of 0's and 1's, such as,
0, 1, 01,
101, or 1100100011100111.
An empty string has no items in it,
i.e., has a length of 0.
Regular expressions can be built using three different operators:
Concatenation (followed-by) - This is expressed by placing
two symbols
(or other regular expressions) adjacent to each other. For example,
01 represents the string of length 2 composed of a zero
followed by a one;
1000001 represents the string of length 7 composed of a
one, followed by five zeros, followed by a one.
Union (or) - This is expressed with the +
symbol.
For example (1 + 0)
matches either 0 or 1. The expression (00) +
(11) matches 00 or 11, while the
expression 0(0+1)
matches either 00 or 01.
Star - The star operator matches any number (including
zero) of
repetitions of the starred item. For example
10* matches 1, 10,
100, 1000, etc.
The expression (10)* matches 10,
1010, 101010, etc. It also matches the
empty string.
Parentheses are used to group operators.
- Consider the regular expression
0*1(0+1)*.- 11. Does this expression match the string
00101100? Does it match the string0000?- 12. Provide an English language description of the set of strings that this expression matches.
- 13. Using JFLAP, design and test an FSA that recognizes the same set of strings as this regular expression. Once you are satisfied that it works, draw it on your lab paper.
- 12. Provide an English language description of the set of strings that this expression matches.
- 11. Does this expression match the string
- Write regular expressions that match the following sets:
- 14. The set of all strings that start with a 1 and end with a 1.
- 15. The set of strings that are accepted by the FSA associated with questions 1 - 4.
- 16. The set of strings that are accepted by the FSA associated with questions 5 - 8.
- 15. The set of strings that are accepted by the FSA associated with questions 1 - 4.
- 14. The set of all strings that start with a 1 and end with a 1.